Litchi Missions vs DJI Fly Missions
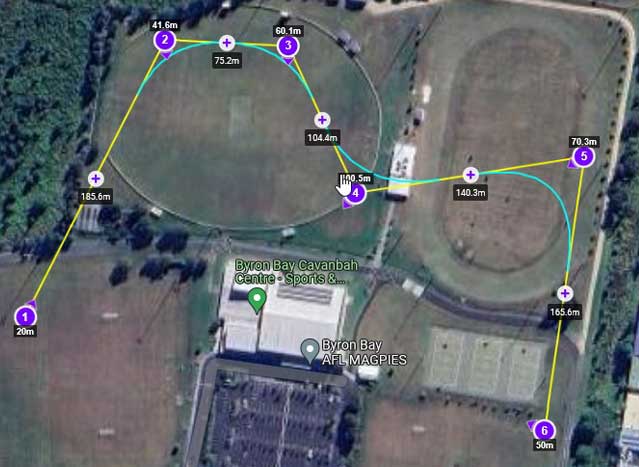
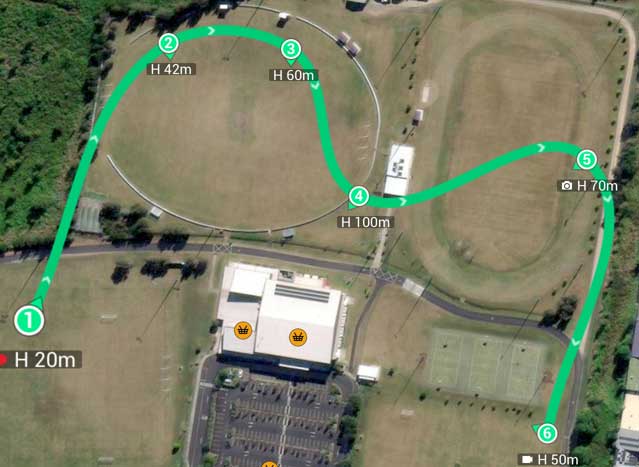
Below are displayed two waypoints missions using the same waypoints. The mission on the left was created with Litchi. The mission on the right was created with DJI Fly.
|
|
Two Types of Missions
There are a number of differences between a Litchi mission and a DJI Fly mission. Some of these differences include:
- Curved Litchi missions do not pass through the interior waypoints while DJI Fly waypoint missions do.
- Litchi supports both curved and straight-line missions while DJI Fly only directly supports curved missions. The WPML language used by DJI does support both straight lines and curves but DJI Fly's implementation only supports the curved setting.
- Litchi enables the curved portions of the missions to be adjusted while the curves in DJI Fly missions are fixed.
- The "Convex Hull" property of Litchi missions means that the mission path is guaranteed to be within the convex hull of the waypoints. DJI Fly missions do not have this property and therefore, DJI's path can travel outside of the convex hull of the waypoints.
Perhaps the most important of those differences is the fact that DJI Fly missions pass through the waypoints while Litchi missions do not.
Obviously, the two products are using different technologies to create flight paths from a set of waypoints. So, the question becomes: "Why?" or "How?". I cannot answer the "Why?". But I can answer the "How?".
Creating Curved Paths: Splines
Creating curves from a set of control points is a very well-understood mathematics problem. This task is done usings splines. However, there are many types of splines, each having their own set of properties. The most popular of these different types include:
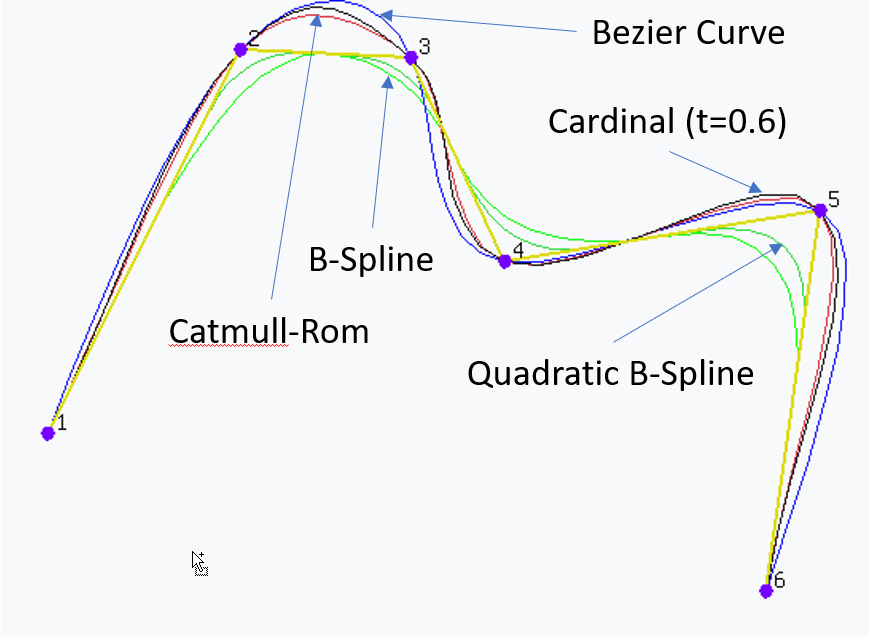
- Quadratic Bézier Curves
- Requires three control points
- Does not pass through the middle control point
- Cubic Bézier Curves
- Requires four control points
- Does not pass through the middle control points
- Can be linked together to form longer, composite curves
- Cardinal Splines
- Requires a minimum of three control points
- Does pass through every control point
- Spline tension or scale is adjustable
- Catmull-Rom Splines
- Requires a minimum of three control points
- Does pass through every control point
- Same as a cardinal spline with the tension set to 0.5
- Comes in "uniform", "centripetal", and "chordal" flavors
- Quadratic B-Splines
- Requires a minimum of three control points
- Does not pass through every control point
- Curve is contained within the convex hull of the control points
- Cubic B-Splines
- Requires a minimum of four control points
- Does not pass through every control point
- Curve is contained within the convex hull of the control points
- The Continuity of Splines (An excellent video describing splines. If you only click on one link on this page, this link should be the one.)
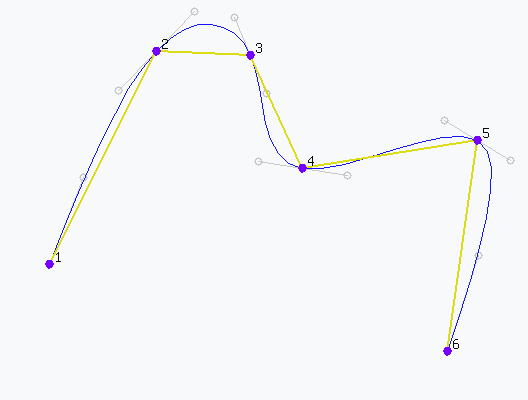
Litchi Mission: Straight Lines with Quadratic B-Splines at the Corners
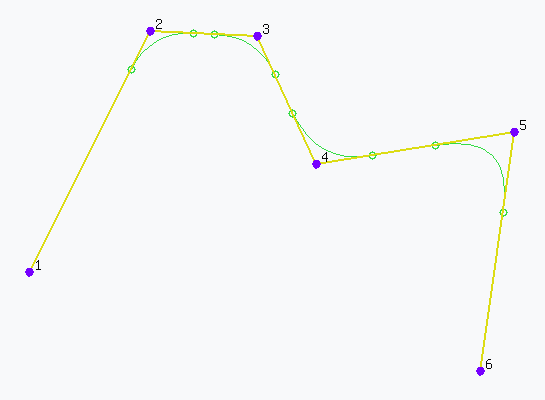
Upon initial inspection, the flight path created using Litchi might appear to be generated using a B-Spline because if follows a similar path to that of a B-Spline. However, Litchi provides a way to adjust the curve size at each waypoint and a B-Spline does not provide that capability.
What Litchi is doing is connecting the waypoints with straight lines and then adding a quadratic spline at each of the interior waypoints. A quadratic spline has three control points. Litchi places the two endpoints of the quadratic spline somewhere on the straight-line path depending on the curve size chosen. The quadratic spline used can be either quadratic B-Spline or a quadratic Bézier curve. They will both produce the same result.
DJI Fly Mission: Centripetal Catmull-Rom Spline
Upon initial inspection, the flight path created using DJI Fly might appear to be generated by using a composite cubic Bézier curve because the curve goes through the waypoints and the composite Bézier is a commonly used method to do this.
A cubic Bézier curve uses exactly four control points and only passes through the first and last of those points. However, it is a common practice to take each pair of consecutive points in a desired curve and fit a Bézier curve to those two waypoints by computing the two inner control points such that the actual waypoints have "C2" continuity with the next Bézier curve. This is called a composite Bézier curve. The process of computing the inner control points is done through the use of the mathematically elegant Gaussian elimination (row reduction) method.
However, upon close inspection, it can be seen that the shape of the spline near its endpoints are not typical of a composite Bézier curve and hint at another type of curve.
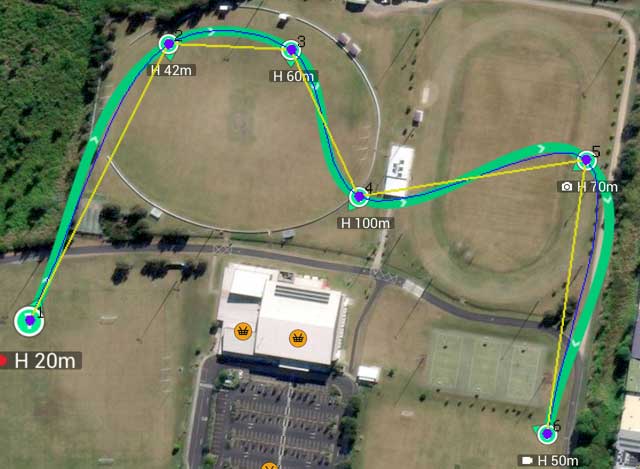
As it turns out, DJI Fly's waypoint path is being generated using a centripetal Catmull-Rom spline where the endpoints are mirrored as indicated by the shape of the path near each endpoint. A Catmull-Rom spline requires that the endpoints are mirrored in order for the curve to reach both endpoints.
The image to the right shows a Centripetal Catmull-Rom spline overlayed onto a DJI Fly mission. Both curves match very closely around the interior points. There is a slight difference near the endpoints which indicate DJI is using different end conditions from a plain Catmull-Rom.